Nota: Para modificar las gráficas es necesario mover la parte que divide la grafica de los datos o bien cambiar los valores manualmente.
Función Lineal
Creación realizada con GeoGebra
Función Cuadrática
Creación realizada con GeoGebra
Función Raíz Lineal
Creación realizada con GeoGebra
Función Raíz Cuadrática
Creación realizada con GeoGebra
Función Racional Lineal
Función Racional Cuadrática
Función Logarítmica
Función Exponencial
Función trigonométrica
miércoles, 24 de noviembre de 2010
jueves, 11 de noviembre de 2010
Funcion cuadratica
La función cuadrática tiene la forma general: f (x) = ax2 + bx + c. El caso más simple es cuando a = 1, b = 0, c = 0 es decir, f (x) = x2 que representa una parábola que pasa por el origen (0, 0). Su gráfica es la siguiente.
El vértice de coordenadas (0, 0) abriendose hacia arriba de manera simétrica al eje y, con dominio Df = (¥, ¥) donde el "(" indica un intervalo abierto, es decir que el valor no se incluye en él, y rango Rf = [0, ¥), donde el "[" indica que el intervalo es cerrado, es decir que el cero está incluido. Retomando la forma general, vemos que en esta función se pueden identificar algunas características generales conociendo algunos parámetros, como por ejemplo el valor del coeficiente principal (es decir el de la variable cuadrática) y el discriminante b2 4ac.
y el discriminante que nos permite saber cuántas veces la gráfica de la parábola cruza el eje x. Observemos la gráfica anterior donde la parábola corta al eje x en un solo punto “el origen”; pero cuando los valores de b y c son distintos de cero, las coordenadas del vértice de la parábola se pueden ubicar en cualquier parte del plano. Y dependiendo de su posición es que pueden o no cortar al eje x. Una manera de saber si la gráfica de la parábola intersecta al eje x o no, es con el uso del discriminante.
En el primer caso si el valor obtenido del discriminante es racional; se puede factorizar con los métodos estudiados en la unidad anterior, en caso contrario se tiene que usar la fórmula general. Por último para hacer una buena gráfica de una función cuadrática (parábola) es conveniente conocer su vértice, este se encuentra en V = (h,k) y se obtiene de la siguiente forma: h = b 2a k = f (h) = a(h)2 + b(h) + c, o sea que para encontrar k, se sustituye el valor de h en la función original.
Funcion lineal
La función lineal es de la forma f (x) = mx + b, donde m representa la pendiente (inclinación)
y b representa la intersección de la recta con el eje y (cuando el valor de x = 0 ) se le
llama ordenada en el origen. La pendiente m puede ser positiva (sube), negativa (baja) o cero
(recta horizontal).
Cuando b = 0 tenemos la funcion f (x) = mx que nos representa una función que pasa
por el origen (0.0).
La pendiente viene a ser intuitivamente “lo que sube o baja la recta entre lo que avanza”.
Tarea 2 Función lineal
Representación gráfica de funciones
En la vida diaria una persona tiene contacto con el concepto de función muy seguido, por
ejemplo. El costo de la electricidad que consume, lo que paga en la gasolinera, la paridad
peso-dólar, etc. Es tan importante este concepto que practicamente podríamos decir que
no hay un lugar en la vida moderna donde no esté presente. Las compañías de seguros, las
empresas automotrices, y casi toda la economía actual se maneja en respuesta a las funciones
que rigen su operación. En el área de ingeniería también es de particular importancia en la
mayoría de las aplicaciones.
Función Lineal
La función lineal es de la forma f (x) = mx + b, donde m representa la pendiente (inclinación)
y b representa la intersección de la recta con el eje y (cuando el valor de x = 0 ) se le
llama ordenada en el origen. La pendiente m puede ser positiva (sube), negativa (baja) o cero
(recta horizontal).
Cuando b = 0 tenemos la funcion f (x) = mx que nos representa una función que pasa
por el origen (0.0).
La pendiente viene a ser intuitivamente “lo que sube o baja la recta entre lo que avanza”.
ejemplo. El costo de la electricidad que consume, lo que paga en la gasolinera, la paridad
peso-dólar, etc. Es tan importante este concepto que practicamente podríamos decir que
no hay un lugar en la vida moderna donde no esté presente. Las compañías de seguros, las
empresas automotrices, y casi toda la economía actual se maneja en respuesta a las funciones
que rigen su operación. En el área de ingeniería también es de particular importancia en la
mayoría de las aplicaciones.
Función Lineal
La función lineal es de la forma f (x) = mx + b, donde m representa la pendiente (inclinación)
y b representa la intersección de la recta con el eje y (cuando el valor de x = 0 ) se le
llama ordenada en el origen. La pendiente m puede ser positiva (sube), negativa (baja) o cero
(recta horizontal).
Cuando b = 0 tenemos la funcion f (x) = mx que nos representa una función que pasa
por el origen (0.0).
La pendiente viene a ser intuitivamente “lo que sube o baja la recta entre lo que avanza”.
miércoles, 3 de noviembre de 2010
Factorizacion
Si un polinomio se escribe como el producto de otros polinomios, cada polinomio del
producto es un factor del polinomio original.
Por ejemplo: Como x2 - 9 = (x + 3)(x - 3), entonces (x + 3) y (x - 3) son factores de
x2 - 9.
La factorización es de gran importancia en numerosas aplicaciones matemáticas, ya que
permite reducir el estudio de expresiones complicadas al estudio de expresiones más simples.
Se pueden determinar propiedades importantes del polinomio x2 - 9, haciendo un
análisis de los factores (x + 3) y (x - 3).
Factorización por Factor Común
La explicación es muy simple, factorizar por Factor Común es aplicar la Ley Distributiva
(Dilema del Mosquetero / 2a. opción) a la inversa, esto es:
Ejercicios
Ejercicios Factorizacion comun.
1.-
2.-
3.-
Factorización por Productos Notables
Factorización de un trinomio cuadrático
Empezando también con la Ley Distributiva (Dilema del Mosquetero) podemos efectuar
el siguiente producto:
Si observamos con cuidado, vemos que el coeficiente del término cuadrático es el producto
de a y c, que son los coeficientes de x en los factores, el término independiente de x es
el producto de b y d, que son los términos independientes de x en los factores; tenemos entonces
dos pares de números y el coeficiente de x es la suma de los resultados al multiplicar
los primeros por los segundos. Esto es:
producto es un factor del polinomio original.
Por ejemplo: Como x2 - 9 = (x + 3)(x - 3), entonces (x + 3) y (x - 3) son factores de
x2 - 9.
La factorización es de gran importancia en numerosas aplicaciones matemáticas, ya que
permite reducir el estudio de expresiones complicadas al estudio de expresiones más simples.
Se pueden determinar propiedades importantes del polinomio x2 - 9, haciendo un
análisis de los factores (x + 3) y (x - 3).
Factorización por Factor Común
La explicación es muy simple, factorizar por Factor Común es aplicar la Ley Distributiva
(Dilema del Mosquetero / 2a. opción) a la inversa, esto es:
Ejercicios
Ejercicios Factorizacion comun.
1.-
2.-
3.-
Factorización por Productos Notables
Factorización de un trinomio cuadrático
Empezando también con la Ley Distributiva (Dilema del Mosquetero) podemos efectuar
el siguiente producto:
Si observamos con cuidado, vemos que el coeficiente del término cuadrático es el producto
de a y c, que son los coeficientes de x en los factores, el término independiente de x es
el producto de b y d, que son los términos independientes de x en los factores; tenemos entonces
dos pares de números y el coeficiente de x es la suma de los resultados al multiplicar
los primeros por los segundos. Esto es:
O sea que haciendo el producto cruzado de a con c, y de b con d se obtiene el coeficiente de x. Ejemplos:
martes, 2 de noviembre de 2010
Polinomios
Adición y sustracción de Polinomios.
Símbolos de agrupación. Los símbolos de agrupación, como son los paréntesis ( ), llaves
{ } y corchetes [ ], se utilizan para señalar, de una manera sencilla, más de una operación.
Recordemos que los paréntesis alteran la jerarquía de los operadores, o sea que las operaciones
entre paréntesis se llevan a cabo primero.
Jerarquía de Operadores: No es necesario utilizar paréntesis cuando el orden en que se
deben efectuar las operaciones cumple con la siguiente jerarquía:
1º. Operadores unitarios y funciones como: Potencia, Raíz, seno, coseno, logarítmica,
exponencial, etc.
2º. Multiplicaciones y divisiones.
3º. Sumas y restas.
Multiplicación y División de polinomios
Además de las leyes básicas de los números reales es conveniente utilizar algunas definiciones
sobre notación y manejo algebraico. Veremos también que algunas propiedades muy
útiles se desprenden de los axiomas.
Ejercicios Multiplicación de polinomios:
1.-
Potencias de Fracciones.
Símbolos de agrupación. Los símbolos de agrupación, como son los paréntesis ( ), llaves
{ } y corchetes [ ], se utilizan para señalar, de una manera sencilla, más de una operación.
Recordemos que los paréntesis alteran la jerarquía de los operadores, o sea que las operaciones
entre paréntesis se llevan a cabo primero.
Jerarquía de Operadores: No es necesario utilizar paréntesis cuando el orden en que se
deben efectuar las operaciones cumple con la siguiente jerarquía:
1º. Operadores unitarios y funciones como: Potencia, Raíz, seno, coseno, logarítmica,
exponencial, etc.
2º. Multiplicaciones y divisiones.
3º. Sumas y restas.
Multiplicación y División de polinomios
Además de las leyes básicas de los números reales es conveniente utilizar algunas definiciones
sobre notación y manejo algebraico. Veremos también que algunas propiedades muy
útiles se desprenden de los axiomas.
Ejercicios Multiplicación de polinomios:
1.-
2.-
3.-
4.-
Propiedad Distributiva.
Potencias de Fracciones.
Álgebra
Indiscutiblemente que lo más importante es entender las propiedades algebraicas, reflexionar
sobre ellas, conectar los conocimientos y tener una preparación sólida. Sin embargo
si no se tiene destreza en el manejo del álgebra, los conceptos teóricos no nos servirián de
mucho; así que en esta unidad pretendemos principalmente que el alumno adquiera la
habilidad mecánica que un alumo de ingeniería ocupa en el aspecto algebraico.
Muchos de los ejercicios, si bien son de mecanización, es importante señalar que se debe
de hacer mención en cada paso algebraico, de la propiedad utilizada o la razón por la que
es posible hacerlo, propiciando así la reflexión, para que el alumno pueda conectar lo que
va haciendo con sus conocimientos previos y que su competencia algebraica vaya creciendo.
Al igual que en los casos anteriores no queremos "enseñar mucho", con dos o tres cosas
que aprenda es bueno: que puedan aplicar la Ley Distributiva (Dilema del Mosquetero), que
puedan factorizar un trinomio y que sepan realizar operaciones con fracciones. Esto es lo
esencial y lo demás lo pueden ir aprendiendo y reforzando en el transcurso del presente y los
próximos semestres. Lo más importante aquí es que puedan identificar en qué situaciones
se aplica y que puedan desarrollar el procedimiento sin error en más del 90% de los casos.
Operaciones algebraicas básicas
Al realizar los ejercicios recomendados
se desarrollará el dominio y la fluidez necesaria para enfrentar con éxito los temas
subsiguientes.
Recordemos que las propiedades básicas de los números reales se pueden resumir en
tres: Reacomodo, Cancelación y Dilema del Mosquetero. Con estas tres como base y algunas
observaciones y aclaraciones vamos a poder desarrollar todos los conocimientos requeridos
Primeramente por el Dilema del Mosquetero (Ley Distributiva de la Multiplicación con
respecto a la Suma), vemos que
(7 + 5)x = 7x + 5x, por lo que si vemos esta propiedad a la inversa tenemos 7x + 5x =
(7 + 5)x = 12x
Esto se le conoce como reducción de términos semejantes.
sobre ellas, conectar los conocimientos y tener una preparación sólida. Sin embargo
si no se tiene destreza en el manejo del álgebra, los conceptos teóricos no nos servirián de
mucho; así que en esta unidad pretendemos principalmente que el alumno adquiera la
habilidad mecánica que un alumo de ingeniería ocupa en el aspecto algebraico.
Muchos de los ejercicios, si bien son de mecanización, es importante señalar que se debe
de hacer mención en cada paso algebraico, de la propiedad utilizada o la razón por la que
es posible hacerlo, propiciando así la reflexión, para que el alumno pueda conectar lo que
va haciendo con sus conocimientos previos y que su competencia algebraica vaya creciendo.
Al igual que en los casos anteriores no queremos "enseñar mucho", con dos o tres cosas
que aprenda es bueno: que puedan aplicar la Ley Distributiva (Dilema del Mosquetero), que
puedan factorizar un trinomio y que sepan realizar operaciones con fracciones. Esto es lo
esencial y lo demás lo pueden ir aprendiendo y reforzando en el transcurso del presente y los
próximos semestres. Lo más importante aquí es que puedan identificar en qué situaciones
se aplica y que puedan desarrollar el procedimiento sin error en más del 90% de los casos.
Operaciones algebraicas básicas
Al realizar los ejercicios recomendados
se desarrollará el dominio y la fluidez necesaria para enfrentar con éxito los temas
subsiguientes.
Recordemos que las propiedades básicas de los números reales se pueden resumir en
tres: Reacomodo, Cancelación y Dilema del Mosquetero. Con estas tres como base y algunas
observaciones y aclaraciones vamos a poder desarrollar todos los conocimientos requeridos
Primeramente por el Dilema del Mosquetero (Ley Distributiva de la Multiplicación con
respecto a la Suma), vemos que
(7 + 5)x = 7x + 5x, por lo que si vemos esta propiedad a la inversa tenemos 7x + 5x =
(7 + 5)x = 12x
Esto se le conoce como reducción de términos semejantes.
Funciones
Es un conjunto de pares ordenados tales que no hay dos pares con el mismo primer
elemento. También se puede expresar como la relación matemática entre el conjunto A y el
conjunto B. Notación f : A -------B.
Dominio de una Función
El conjunto de los primeros elementos en los pares ordenados en una función f se llama
Dominio y se denota: DOM( f ) y el conjunto formado por los segundos elementos se llama
Rango y su notación es: RAN( f ).
Si consideramos la función como una relación, a cada elemento del dominio le corresponde
un elemento único del rango, sin embargo para un elemento del rango podría
haber varios elementos del dominio. Si a un elemento del dominio le llamamos x entonces
el correspondioente elemento del rango se denota por f (x).
elemento. También se puede expresar como la relación matemática entre el conjunto A y el
conjunto B. Notación f : A -------B.
Dominio de una Función
El conjunto de los primeros elementos en los pares ordenados en una función f se llama
Dominio y se denota: DOM( f ) y el conjunto formado por los segundos elementos se llama
Rango y su notación es: RAN( f ).
Si consideramos la función como una relación, a cada elemento del dominio le corresponde
un elemento único del rango, sin embargo para un elemento del rango podría
haber varios elementos del dominio. Si a un elemento del dominio le llamamos x entonces
el correspondioente elemento del rango se denota por f (x).
lunes, 1 de noviembre de 2010
Expresión algebraica y polinomios
Polinomios.
En secundaria y preparatoria se conoce un polinomio como una expresión algebraica con
varios términos, si es monomio con un término, si es binomio con dos, trinomio con tres y
polinomio no se con cuántos pero deben ser muchos. Sin embargo desde el punto de vista de
matemáticas y su manejo formal un polinomio es una expresión algebraica donde aparecen
únicamente sumas, diferencias o productos de números reales o variables. Podemos también
dar una definición formal.
Definición. Un polinomio de una variable de grado n, es una expresión de la forma
Ejemplo de no polinomios.
1.
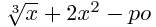
2.
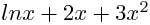
3.
Raiz Cuadrada. (Formula)
1.-
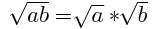
2.-
3.-
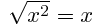
Raiz Cuadrada. (Ejercicios)
1.-
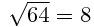
2.-
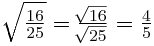
3.-
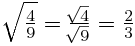
4.-
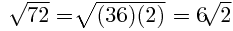
Ejercicio: Identificar si la expresión es polinomio. Si es polinomio encontrar el grado.
2.-Si, grado 2
3.-Si, grado 1
4.-Si, grado 2
5.-Si, grado 2
6.-Si, polinomio grado 2
Conceptos Matematicos
Resta y división
La operación de sustracción o resta a - b en el conjunto de los números reales R, esta
definida mediante la adición del inverso aditivo de b, es decir: a - b = a + (-b)
Por ejemplo para el conjunto de los números naturales N = f1, 2, 3, ...glos inversos se
representan como N = { f -1, -2, -3, ...} y así, agregando el cero, se forma el conjunto de los
enteros. Z = { f..., -3, -2, -1, 0, 1, 2, 3, ...}
Como la resta es sumar el inverso, cuando tenemos expresiones algebraicas con sumas y
restas, las restas las tomamos como sumas (de inversos) y podemos tratarlas prácticamente
igual que las sumas. Por ejemplo a(b - c) = ab - ac por lo que la Ley Distributiva de la
suma también se cumple para la resta. De este modo no tenemos que estar aprendiendo
nuevas reglas para la operación de resta.
La división de a entre b, se define como el producto de a por el inverso multiplicativo de :
División y el cero:
(1).
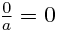
(2). no esta definida
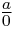
(3). indeterminado (tampoco está definido)
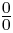
La operación de sustracción o resta a - b en el conjunto de los números reales R, esta
definida mediante la adición del inverso aditivo de b, es decir: a - b = a + (-b)
Por ejemplo para el conjunto de los números naturales N = f1, 2, 3, ...glos inversos se
representan como N = { f -1, -2, -3, ...} y así, agregando el cero, se forma el conjunto de los
enteros. Z = { f..., -3, -2, -1, 0, 1, 2, 3, ...}
Como la resta es sumar el inverso, cuando tenemos expresiones algebraicas con sumas y
restas, las restas las tomamos como sumas (de inversos) y podemos tratarlas prácticamente
igual que las sumas. Por ejemplo a(b - c) = ab - ac por lo que la Ley Distributiva de la
suma también se cumple para la resta. De este modo no tenemos que estar aprendiendo
nuevas reglas para la operación de resta.
La división de a entre b, se define como el producto de a por el inverso multiplicativo de :
División y el cero:
(1).
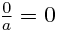
(2). no esta definida
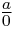
(3). indeterminado (tampoco está definido)
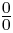
Ver las divisiones como multiplicaciones por un inverso es muy útil al igual que la resta,
porque podemos extrapolar varias de las operaciones y conceptos básicos de la multiplicación
a la división. Así por ejemplo a+b/c = a/c+ b/c, debido a que c, al estar dividiendo, está
implicando en realidad una multiplicación (considerando su inverso) por lo tanto se cumple
la Ley Distributiva (Dilema del Mosquetero, 2a. opción).
Suscribirse a:
Comentarios (Atom)





















