Conceptos Matematicos

Resta y división
La operación de sustracción o resta a - b en el conjunto de los números reales R, esta
definida mediante la adición del inverso aditivo de b, es decir: a - b = a + (-b)
Por ejemplo para el conjunto de los números naturales N = f1, 2, 3, ...glos inversos se
representan como N = { f -1, -2, -3, ...}  y así, agregando el cero, se forma el conjunto de los
enteros. Z = { f..., -3, -2, -1, 0, 1, 2, 3, ...}
Como la resta es sumar el inverso, cuando tenemos expresiones algebraicas con sumas y
restas, las restas las tomamos como sumas (de inversos) y podemos tratarlas prácticamente
igual que las sumas. Por ejemplo a(b - c) = ab - ac por lo que la Ley Distributiva de la
suma también se cumple para la resta. De este modo no tenemos que estar aprendiendo
nuevas reglas para la operación de resta.

La división de a entre b, se define como el producto de a por el inverso multiplicativo de :

División y el cero:
(1).





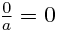
(2).  no esta definida





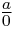
(3). indeterminado (tampoco está definido)

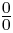
Ver las divisiones como multiplicaciones por un inverso es muy útil al igual que la resta,

porque podemos extrapolar varias de las operaciones y conceptos básicos de la multiplicación

a la división. Así por ejemplo a+b/c = a/c+ b/c, debido a que c, al estar dividiendo, está

implicando en realidad una multiplicación (considerando su inverso) por lo tanto se cumple

la Ley Distributiva (Dilema del Mosquetero, 2a. opción).